Chapter 3
The Discrete Laplace Operators: L2LC, L3LC and L3ALC

3.1  Introduction

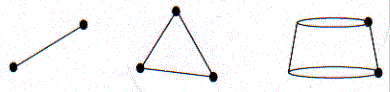
The Fortran subroutines described in this manual are useful in the implementation of integral equation methods for the solution of the general two-dimensional, the general three-dimensional and the axisymmetric three-dimensional Laplace equation, which governs f(p) in a given domain. The subroutines compute the discrete form of the integral operators L, M, M^t and N that arise in the application of collocation to integral equation formulations of the Laplace equation. Expressions for the discrete integral operators are derived by approximating the boundaries by the most simple elements for each of the three cases - straight line elements for the general two-dimensional case, flat triangular elements for the general three-dimensional case and conical elements for the axisymmetric three-dimensional case - and approximating the boundary functions by a constant on each element. The elements are illustrated in figure 3.1.

The Laplace Integral Operators

3.1.2  The L*LC Subroutines

For each particular case of boundary division, the discrete form of the operators is computed using the subroutines L2LC (two-dimensional), L3LC (three-dimensional) and L3ALC (axisymmetric three-dimensional). The subroutines are thus useful for the solution of the interior or exterior Laplace via integral equation methods; the subroutines compute the matrix elements in the linear systems of equations that arise. Each subroutine is meant to be used as a tool that will be called many times within a main program.

The objective here is to describe the underlying methods employed in computing the discrete form of the integral operators (12)-(15), to outline the Fortran subroutines and explain how the subroutines may be utilised and to demonstrate the subroutines. The subroutines have been written to the Fortran 77 standard and employ double-precision arithmetic.

The subroutines' parameter list have the following general form:

SUBROUTINE L{2 or 3 or 3A } LC(

point (p and the unit vector v_p, if necessary),

geometry of the element (vertices which define element),

quadrature rule (weights and abscissae for the standard element),

validation and control parameters,

discrete Laplace integral operators (output) ).